ΤΟ ΤΕΛΕΥΤΑΙΟ ΘΕΩΡΗΜΑ ΤΟΥ FERMAT

 

ΚΑΘΗΜΕΡΙΝΑ Ο ΕΡΝΤΟΓΑΝ ΦΩΤΟΓΡΑΦΙΖΕΤΑΙ ΜΠΡΟΣΤΑ ΣΕ ΟΠΛΑ ΠΟΥ ΚΑΤΑΣΚΕΥΑΖΟΥΝ ΟΙ ΙΔΙΟΙ ΟΙ ΤΟΥΡΚΟΙ. ΚΑΘΗΜΕΡΙΝΑ Ο ΜΗΤΣΟΤΑΚΗΣ ΦΩΤΟΓΡΑΦΙΖΕΤΑΙ ΣΤΙΣ ΑΤΕΛΕΙΩΤΕΣ ΔΙΑΚΟΠΕΣ ΤΟΥ ΜΑΖΙ ΜΕ ΤΗΝ ΟΙΚΟΓΕΝΕΙΑ ΤΟΥ ΚΑΙ ΤΑ ΑΤΕΛΕΙΩΤΑ ΓΚΑΡΣΟΝΙΑ ΠΟΥ ΤΟΝ ΥΠΗΡΕΤΟΥΝ. Τουρκία: Ο Στρατός παρέλαβε τα πρώτα έξι βελτιωμένα αυτοκινούμενα πυροβόλα T-155 Firtina-2.

"Γύρω στα 1630, ο Fermat μελέτησε τα Αριθμητικά του Διόφαντου του Αλεξανδρέως, ένα έργο που πιθανότατα γράφτηκε τον 3ο αιώνα μ.Χ. και αναφέρεται σε διάφορα προβλήματα των οποίων οι λύσεις είναι ακέραιοι ή γενικότερα ρητοί αριθμοί. Ο Fermat έγραψε πολυάριθμα σχόλια στο περιθώριο του αντιτύπου των Αριθμητικών που διέθετε. Το σχόλιο που μας αφορά ειδικότερα αναφέρεται στο Πρόβλημα 8 του Βιβλίου 2, όπου ο Διόφαντος θέτει το εξής ζήτημα: « Τον επιταχθέντα τετράγωνον διελείν εις δυο τετραγώνους» (δοθέντος ενός τελείου τετραγώνου, να το αναλύσετε ως άθροισμα δυο τελείων τετραγώνων).
Η σημείωση του Fermat, μεταφρασμένη από τα λατινικά, αναφέρει: «Είναι αδύνατον να αναλύσουμε έναν κύβο σε δυο τέλειους κύβους ή γενικά, κάθε δύναμη μεγαλύτερη της δευτέρας σε δυο δυνάμεις ίδιου βαθμού. Έχω ανακαλύψει μια πραγματικά θαυμάσια απόδειξη, αλλά το περιθώριο αυτό είναι πολύ στενό για να τη χωρέσει»."

O Andrew Wiles,  (Άντριου Γουάιλς),  γεννημένος 11 Απριλίου του 1953  είναι ο μαθηματικός που απέδειξε το τελευταίο θεώρημα του Fermat το 1995, ένα πρόβλημα που παρέμενε άλυτο για πάνω από 350 χρόνια. Μπορεί να βρεθούν απλούστερες αποδείξεις του θεωρήματος (π.χ. Fermat’s Last Theorem and More Can Be Proved More Simply), όμως ο Andrew Wiles θα παραμείνει στην ιστορία ως εκείνος που το απέδειξε πρώτος.

O καθηγητής Andrew Wiles περιέγραψε την επτάχρονη αναζήτηση του «Ιερού Δισκοπότηρου» των μαθηματικών ως εξής:
«Ίσως, ο καλύτερος τρόπος για να περιγράψω την εμπειρία μου στα μαθηματικά είναι να την παρομοιάσω με την εμπειρία του να εισέρχεσαι σε ένα σκοτεινό μέγαρο. Εισέρχεσαι στο πρώτο σκοτεινό, απολύτως σκοτεινό, δωμάτιο.
Σκοντάφτεις δεξιά – αριστερά και πέφτεις επάνω στα έπιπλα. Σιγά σιγά μαθαίνεις που βρίσκεται κάθε έπιπλο. Και τελικά, μετά από περίπου έξι μήνες, βρίσκεις το διακόπτη και ανάβεις το φως. Ξαφνικά, λοιπόν, τα πάντα φωτίζονται και βλέπεις πλέον που βρισκόσουν. Κατόπιν εισέρχεσαι στο επόμενο σκοτεινό δωμάτιο …»

 

Στη συνέχεια μπορείτε
να δείτε ένα ντοκιμαντέρ διάρκειας πενήντα λεπτών που γυρίστηκε για το BBC από τον Simon Singh το 1996,
και να διαβάσετε ένα πολύ κατατοπιστικό άρθρο που δημοσιεύθηκε στο περιοδικό QUANTUM, Μάρτιος/Απρίλιος 1997, Τόμος 4/Τεύχος 2
και τα δυο σχετικά με την απόδειξη του περίφημου «τελευταίου θεωρήματος του Fermat» από τον Wiles.

Το ντοκιμαντέρ του Simon Singh:

Το άρθρο που ακολουθεί δημοσιεύθηκε στο περιοδικό QUANTUM το 1997 και αποτελεί σύνθεση τμημάτων των άρθρων «Fermat’s Last Theorem and Modern Arithmetic» των K. A. Ribet και B. Hayes (Αmerican Scientist, Μάρτιος/Απρίλιος 1994), «Andrew Wiles: A Math Ehiz Battles 350 – Year – Old Puzzle» της G. Kolata (Math Horizons, Χειμώνας 1993), και τμημάτων του Κεφαλαίου 3 του βιβλίου From Here to Infinity του Ian Stewart (Oxford University Press, 1996) σε μετάφραση του Κώστα Γαβρά, μαθηματικού και του Φάνη Γραμμένου, φυσικού.

Το τελευταίο θεώρημα του Fermat

Στο περιθώριο των Αριθμητικών του Διοφάντου ο Fermat διατύπωσε ένα θεώρημα που το άφησε αναπόδεικτο, λόγω … έλλειψης χώρου. Ο Andrew Wiles συμπλήρωσε αυτό το κενό.
O Eric Temple Bell, o ο μαθηματικός και βιογράφος πολλών μαθηματικών πίστευε ότι το τελευταίο θεώρημα του Fermat θα ήταν ένα από τα ερωτήματα που θα παρέμεναν αναπάντητα, ακόμα και τη μέρα που ο ανθρώπινος πολιτισμός θα αυτοκαταστρεφόταν σ’ έναν πυρηνικό πόλεμο.

Η περίφημη σημείωση του Pierre de Fermat βρίσκεται στην έκδοση των Αριθμητικών του Διοφάντου από τον γιο του Fermat, τον Samuel. Ο Fermat είχε διαβάσει τα Αριθμητικά στην πρώτη σύγχρονη έκδοσή τους – όπως δημοσιεύθηκαν το 1621 από τον Claude-Gaspar Bachet – , όμως το αντίτυπο με τις παρατηρήσεις του δεν έχει ανακαλυφθεί ακόμη. Ο Samuel Fermat, στην έκδοσή του έχει αντιγράψει τη σημείωση και την παραθέτει κάτω από το λατινικό και το ελληνικό κείμενο του Προβλήματος 8 του βιβλίου 2.

Ο Bell διατύπωσε αυτή την πρόβλεψη λίγο πριν από το θάνατό του, το 1960. Αν ζούσε λίγες δεκαετίες ακόμη, θα είχε ιδιαίτερο ενδιαφέρον να δούμε τι θα τον εξέπληττε περισσότερο: το γεγονός ότι η ανθρωπότητα συνεχίζει να επιβιώνει ή το ότι ανακοινώθηκε η απόδειξη του εν λόγω θεωρήματος;
Το ίδιο θεώρημα διατυπώνεται εύκολα. Ο Pierre de Fermat ισχυρίστηκε ότι, εάν a, b και c είναι θετικοί ακέραιοι αριθμοί και αν n είναι ακέραιος μεγαλύτερος του 2, τότε η εξίσωση
aⁿ + bⁿ = cⁿ
είναι αδύνατη.
Η απλότητα της διατύπωσης είναι απατηλή: η πρόταση είχε αντισταθεί σε όλες τις απόπειρες απόδειξης για περισσότερο από 350 χρόνια. Και η πρόσφατη απόδειξη, την οποία επινόησε ο Andew Wiles του Πανεπιστημίου του Πρίνστον, απαιτεί για την προσέγγιση του προβλήματος ένα εξαιρετικό οπλοστάσιο μαθηματικών εργαλείων και τεχνικών. Η απόδειξη του Wiles εμπεριέχεται σ’ ένα πυκνό και δύσκολο χειρόγραφο 200 σελίδων, το οποίο ενσωματώνει μέσω παραπομπών μια κατά πολύ μεγαλύτερη ποσότητα μαθηματικού έργου που αναπτύχθηκε τα τελευταία τριάντα ή και περισσότερα χρόνια.
Είναι σημαντικό να καταλάβουμε την πραγματική θέση που κατέχει στα σύγχρονα μαθηματικά το τελευταίο θεώρημα του Fermat: είναι ένα διάσημο αίνιγμα, αλλά μετά δυσκολίας μπορεί να χαρακτηριστεί ως μια πρόταση κεντρικής ή θεμελιώδους σπουδαιότητας.
Η απόδειξη του θεωρήματος δεν σημαίνει ότι θα μας οδηγήσει σε πολλά μαθηματικά συμπεράσματα μεγάλου ενδιαφέροντος. Από την άλλη, η αναζήτηση μιας απόδειξής του έχει συνεισφέρει στην ανάπτυξη μαθηματικών γνώσεων μεγάλης σπουδαιότητας. Ειδικότερα, ο Wiles προσέγγισε το πρόβλημα ξεκινώντας να αποδείξει μιαν άλλη πρόταση, γνωστή ως εικασία των Taniyama – Shimura , από την οποία το τελευταίο θεώρημα του Fermat έπεται ως πόρισμα.
Η εικασία των Taniyama – Shimura είναι βαθύτερη και ενδεχομένως πιο σημαντική από το ίδιο το τελευταίο θεώρημα του Fermat. Ανήκει σ’ ένα πεδίο μαθηματικών που αναπτύσσεται ραγδαία τις τελευταίες τρεις δεκαετίες, χωρίς ωστόσο να προκαλεί μεγάλο ενδιαφέρον στους χώρους πέραν του μαθηματικού επαγγέλματος. Το πεδίο αυτό ονομάζεται «αριθμητική αλγεβρική γεωμετρία» ή «μοντέρνα αριθμητική» προήλθε από την προσπάθεια εφαρμογής μεθόδων των σύγχρονων μαθηματικών στη μελέτη προβλημάτων, γνωστών ως διοφαντικών προβλημάτων, στα οποία ο σκοπός είναι η εύρεση όλων των ακεραίων λύσεων μιας οικογένειας εξισώσεων. Η σύγχρονη αριθμητική διαθέτει αυτή καθ’ εαυτή πλούσια δομή και φαίνεται να συνδέεται, με τον έναν ή τον άλλο τρόπο, με κάθε άλλο κλάδο των μαθηματικών. Είναι αξιοσημείωτο το γεγονός ότι το αφηρημένο οπλοστάσιο αυτού του κλάδου έχει οδηγήσει σε μια νέα κατανόηση του πλέον διάσημου όλων των διοφαντικών προβλημάτων – του τελευταίου θεωρήματος του Fermat.

Σημειώσεις στο περιθώριο

Η ιστορία περί του πως ο Fermat πρότεινε το τελευταίο θεώρημά του είναι γνωστή, αλλά είναι τόσο καλή ώστε δεν μπορούμε παρά να την αναφέρουμε για άλλη μια φορά. O Pierre de Fermat γεννήθηκε στη νότια Γαλλία το 1601 και πέρασε το μεγαλύτερο μέρος της ζωής του στην Τουλούζη, όπου εργάστηκε ως διακεκριμένος νομικός στη δημόσια διοίκηση, υπηρετώντας τον Λουδοβίκο τον ΙΔ’.
Ως μαθηματικός υπήρξε ερασιτέχνης, αλλά με ιδιαίτερα καλές γνωριμίες και επαφές διατηρούσε εκτεταμένη αλληλογραφία με τους Rene Descartes, Blaise Pascal και άλλους φωστήρες της εποχής. Πράγματι, η κύριά μας πηγή γνώσης γύρω από το μαθηματικό του έργο είναι η αλληλογραφία του – καθώς και οι σημειώσεις του στο περιθώρια των βιβλίων.
Γύρω στα 1630, ο Fermat μελέτησε τα Αριθμητικά του Διόφαντου του Αλεξανδρέως, ένα έργο που πιθανότατα γράφτηκε τον 3ο αιώνα μ.Χ. και αναφέρεται σε διάφορα προβλήματα των οποίων οι λύσεις είναι ακέραιοι ή γενικότερα ρητοί αριθμοί. Ο Fermat έγραψε πολυάριθμα σχόλια στο περιθώριο του αντιτύπου των Αριθμητικών που διέθετε. Το σχόλιο που μας αφορά ειδικότερα αναφέρεται στο Πρόβλημα 8 του Βιβλίου 2, όπου ο Διόφαντος θέτει το εξής ζήτημα: « Τον επιταχθέντα τετράγωνον διελείν εις δυο τετραγώνους» (δοθέντος ενός τελείου τετραγώνου, να το αναλύσετε ως άθροισμα δυο τελείων τετραγώνων).
Η σημείωση του Fermat, μεταφρασμένη από τα λατινικά, αναφέρει: «Είναι αδύνατον να αναλύσουμε έναν κύβο σε δυο τέλειους κύβους ή γενικά, κάθε δύναμη μεγαλύτερη της δευτέρας σε δυο δυνάμεις ίδιου βαθμού. Έχω ανακαλύψει μια πραγματικά θαυμάσια απόδειξη, αλλά το περιθώριο αυτό είναι πολύ στενό για να τη χωρέσει».
Ο βασανιστικός υπαινιγμός για μια απόδειξη που κάποτε υπήρξε γνωστή αλλά χάθηκε στη συνέχεια έχει αναμφίβολα συνεισφέρει στη δημοφιλή ρομαντική ιστορία γύρω από το τελευταίο θεώρημα του Femat. Έτσι προέκυψε ο χαρακτηρισμός «τελευταίο», για τον οποίο ο Fermat δεν φέρει καμιά ευθύνη. Ασφαλώς το θεώρημα δεν ήταν το τελευταίο που πρότεινε κατά τη διάρκεια της ζωής του. Έζησε έως το 1865, συνεισφέροντας πολλά ακόμη στα μαθηματικά. Η ονομασία «τελευταίο» εμφανίστηκε τον 18ο ή 19ο αιώνα, και μάλλον στόχευε στην αναγνώριση του θεωρήματος ως της τελευταίας πρότασης του Fermat που θα παρέμενε είτε αυταπόδεικτη είτε χωρίς αντιπαράδειγμα.
Διέθετε πράγματι ο Fermat μια «θαυμάσια» απόδειξη, την οποία θα μπορούσε να είχε γράψει αν το περιθώριο ήταν λίγο μεγαλύτερο; Πρόκειται για ακόμη ένα από εκείνα τα ερωτήματα που έχουν σοβαρή πιθανότητα να διαρκέσουν περισσότερο από τον ανθρώπινο πολιτισμό.
Μια πιθανή απάντηση είναι ότι ο Fermat νόμισε πως είχε καταλήξει σε μια απόδειξη, αργότερα όμως ανακάλυψε σ’ αυτήν κάποια ατέλεια. Σε μεταγενέστερες επιστολές προς συναδέλφους του, ο Fermat παρέπεμψε σε αποδείξεις των ειδικών περιπτώσεων για n=3 και n=4, αλλά τη γενική απόδειξη δεν τη μνημόνευε ποτέ ξανά.

Πρώιμες προσπάθειες

Η ανεύρεση ακέραιων λύσεων της εξίσωσης
aⁿ + bⁿ = cⁿ
δεν είναι δύσκολη όταν n=1 καθώς, στην περίπτωση αυτή, η εξίσωση ανάγεται στην απλή μορφή
a + b = c
Επειδή το άθροισμα οποιωνδήποτε δυο ακεραίων είναι επίσης ακέραιος αριθμός, για κάθε a και b υπάρχει πάντοτε ένας c που ικανοποιεί την εξίσωση.
Όταν n=2 (η περίπτωση που εξέτασε ο Διόφαντος), το πρόβλημα γίνεται ελάχιστα δυσκολότερο. Βεβαίως, η εξίσωση
a² + b² = c²
είναι ο τύπος του Πυθαγόρα, η οποία συνδέει τις κάθετες πλευρές και την υποτείνουσα ενός ορθογωνίου τριγώνου, και επιδέχεται άπειρες το πλήθος ακέραιες λύσεις – αρχής γενομένης από τη γνωστή
3² + 4² = 5²
Αιώνες πριν τον Διόφαντο, ο Ευκλείδης έδωσε μια μέθοδο σχηματισμού όλων των συνόλων τέτοιων πυθαγόρειων τριάδων.
Με δεδομένη την απειρία λύσεων όταν n=1 ή n=2 η πιθανότητα να μην υπάρχει καμιά ακέραιη λύση για όλα τα n≥3 φαίνεται να εκπλήσσει, όμως αυτός είναι ο ισχυρισμός του Fermat.
Ο ίδιος ο Fermat απέδειξε το θεώρημα για την περίπτωση n=4 (και αυτή τη φορά ανέπτυξε την επιχειρηματολογία του σε μια άλλη σημείωση στο περιθώριο).

Ο Pierre de Fermat http://en.wikipedia.org/wiki/Pierre_de_Fermat (1601 – 1665) υπήρξε διακεκριμένος νομικός, αλλά κέρδισε την αθανασία χάρη σ’ ένα χόμπι του: τα μαθηματικά

Ουσιαστικά, ο Fermat απέδειξε μια ελαφρώς γενικότερη πρόταση, δείχνοντας ότι η εξίσωση
a⁴ + b⁴ = c²
δεν επιδέχεται ακέραιες λύσεις• αφού κάθε τέλεια τέταρτη δύναμη είναι επίσης και τέλειο τετράγωνο, το αποτέλεσμα αυτό συνεπάγεται την ορθότητα του αρχικού θεωρήματος για n=4. Για να το διατυπώσουμε διαφορετικά, ο Fermat έδειξε ότι δεν υπάρχουν πυθαγόρειες τριάδες
a² + b² = c²
όπου τα ίδια τα a, b να είναι τέλεια τετράγωνα.
Η ιδέα στην οποία βασίζεται η απόδειξη αποτελεί μια τεχνική που επινόησε ο Fermat και ονομάζεται μέθοδος της άπειρης καθόδου. Αφετηρία είναι η υπόθεση ότι υπάρχουν πράγματι ακέραιες λύσεις της εξίσωσης
a⁴ + b⁴ = c².
Ο Fermat ανακάλυψε μια σειρά πράξεων με τις οποίες, δοθείσης μιας οιασδήποτε τέτοιας λύσης, δημιουργείται μία μικρότερή της. Η εφαρμογή της ίδιας ακολουθίας πράξεων στη νέα λύση έχει ως αποτέλεσμα μία ακόμα μικρότερη λύση. Η διαδικασία αυτή μπορεί να συνεχιστεί απεριόριστα, δημιουργώντας μια απειροσειρά από ολοένα μικρότερες λύσεις. Η ύπαρξη όμως μιας τέτοιας σειράς από συνεχώς μικρότερους αριθμούς είναι αδύνατη στο σύνολο των θετικών ακεραίων, το οποίο διαθέτει ένα καλώς ορισμένο κάτω φράγμα (τον αριθμό 1). Ο μόνος τρόπος αποφυγής αυτού του ατόπου είναι η απόρριψη της αρχικής υπόθεσης περί ύπερξης ακέραιης λύσης.
Η περίπτωση n=3 εξετάστηκε από τον Leonard Euler εξετάστηκε, τον μεγάλο ελβετό μαθηματικό του 18ου αιώνα. Και η δική του απόδειξη βασίζεται στην άπειρη κάθοδο, αλλά είναι περισσότερο πεπλεγμένη από την απόδειξη για n=4. Στα χρόνια που ακολούθησαν, αποδείχθηκαν αρκετές ειδικές περιπτώσεις του τελευταίου θεωρήματος του Fermat. Γύρω στα 1820, ο Γάλλος Adrien – Marie Legendre και ο Γερμανός P. G. Lejeune Dirichlet έδωσαν αποδείξεις για την περίπτωση n=5. Ο Dirichlet προσπάθησε να αποδείξει και την περίπτωση n=7, αλλά τελικά το κατόρθωσε μόνο για n=14• η απόδειξη για n=7 επινοήθηκε αργότερα, από τον Γάλλο Gabriel Lame. Τότε, το 1847, διατυπώθηκε μια σημαντική πρόοδος από τον Γερμανό Ernst E. Kummer, ο οποίος έφτασε πολύ κοντά σε μια γενική απόδειξη του θεωρήματος. Το έργο του Kummer αποδείκνυε ότι το τελευταίο θεώρημα του Fermat αληθεύει αληθεύει για άπειρο πλήθος εκθετών, συγκεκριμένα για όλες τις τιμές του n που διαιρούνται από «κανονικούς» πρώτους αριθμούς. Οι τελευταίοι αποτελούν ένα υποσύνολο των πρώτων αριθμών (δηλαδή των θετικών ακεραίων που διαιρούνται μόνο από τον εαυτό τους και τη μονάδα). Οι μόνοι μη κανονικοί πρώτοι, μικρότεροι του 100, είναι οι 37, 59 και 67, αλλά ο Kummer πέτυχε στην πορεία να επινοήσει την απόδειξη και γι’ αυτές τις ειδικές τιμές. Έτσι, το τελευταίο θεώρημα του Fermat είχε αποδειχτεί για όλα τα n<100.
Tα τελευταία χρόνια, μελέτες με τη βοήθεια υπολογιστών είχαν πετύχει μεγάλη ανύψωση του κάτω ορίου κάθε δυνατού αντιπαραδείγματος. Ένα αποτέλεσμα που δημοσιεύθηκε τον Ιούλιο του 1993 (από τους Buhler, Crandall, Ernvall Metsänkylä) δείχνει ότι το τελευταίο θεώρημα του Fermat αληθεύει για όλους τους εκθέτες n<4.000.000, οπότε κάθε ακέραιη λύση της
aⁿ + bⁿ = cⁿ
θα έπρεπε να αποτελείται από αστρονομικά μεγάλους ακεραίους. (Αποδεικνύεται ότι η μικρότερη δυνατή τιμή του cⁿ θα ήταν ένας αριθμός με περισσότερα από 26 εκατομμύρια δεκαδικά ψηφία.) Εντούτοις, δεν υπήρξε μαθηματικός που να θεώρησε το θέμα λήξαν μόνο και μόνο επειδή εξαντλήθηκε ένας πεπερασμένος αριθμός περιπτώσεων. Υπάρχει άπειρο πλήθος από τους μη κανονικούς πρώτους αριθμούς του Kummer, συνεπώς όσο και να επεκτεινόταν η κατά περίπτωση ανάλυση, θα ήταν αδύνατον να οδηγήσει σε ολοκληρωμένο αποτέλεσμα.

Η εικασία Taniyama
O δρ. Andrew Wiles είναι ήσυχος και πράος άνθρωπος, μ’ ένα ντροπαλό χαμόγελο. Ωστόσο, βρήκε το κουράγιο να επενδύσει επτά χρόνια εργαζόμενος μυστικά στο πλέον διάσημο μαθηματικό πρόβλημα και αντιμετωπίζοντας μια τρομερή πρόκληση που έφερε σε αμηχανία τους καλύτερους μαθηματικούς επί περισσότερο από 300 χρόνια. Στις 23 Ιουνίου του 1993, και παρ’ όλες τις αντιξοότητες, ο Wiles ήταν σε θέση να αναγγείλει ότι βρήκε τη λύση του προβλήματος. Ήταν ένα επίτευγμα το οποίο, εάν αλήθευε, θα εκτόξευε τον σαραντάχρονο τότε καθηγητή μαθηματικών του Πανεπιστημίου του Πρίνστον στο στρατόπεδο των γιγάντων αυτού του γνωστικού πεδίου: ο Wiles θα έφτανε στον κολοφώνα της δόξας του δημιουργώντας ένα είδος ινδάλματος στην επιστημονική κοινότητα.
Η απόδειξη του Wiles για το τελευταίο θεώρημα του Fermat δεν είναι του είδους που μπορεί να γραφεί σ’ ένα φύλλο χαρτί. Μάλιστα απαιτεί πολύ ειδικές γνώσεις για την πλήρη κατανόησή της. Ωστόσο, οι γενικές γραμμές της απόδειξης είναι κατανοητές, κι έτσι στη συνέχεια θα προσπαθήσουμε να δώσουμε μια ιδέα αυτής της δραματικής εξέλιξης στη θεωρία αριθμών.
Το αποφασιστικό σημείο στην ιστορία μας εμφανίστηκε περίπου πριν μια δεκαετία, το 1985, όταν ο δρ. Gerhard Frey του Πανεπιστημίου της Σάαρλαντ της Γερμανίας ισχυρίστηκε ότι το τελευταίο θεώρημα του Fermat θα προέκυπτε αυτομάτως αν αλήθευε μια άλλη, φαινομενικά άσχετη με αυτό πρόταση, η εικασία του Taniyama (ή εικασία Τaniyama – Shimura – Weil – όνομα που οφείλεται στο γεγονός ότι το 1955 ο Taniyama έθεσε κάποια ερωτήματα τα οποία γενικεύθηκαν και έγιναν ακριβέστερα από τους Shimura και Weil). Η πρόταση αυτή αναφέρεται στις ελλειπτικές καμπύλες, δηλαδή μια κλάση κυβικών εξισώσεων οι οποίες είχαν μελετηθεί σε βάθος από τον ίδιο τον Fermat, αν και όχι σε σχέση με το θεώρημά του ….

(….) Μπορούμε να εννοήσουμε τη γενική ιδέα που κρύβει η εικασία του Taniyama, θεωρώντας μια πολύ ειδική περίπτωση. Υπάρχει μια ιδιαίτερη στενή σχέση μεταξύ της εξίσωσης του Πυθαγόρα
a² + b² = c²,
του κύκλου μοναδιαίας ακτίνας και των τριγωνομετρικών συναρτήσεων του ημιτόνου και του συνημιτόνου. Μπορούμε να συναγάγουμε την αναφερόμενη σχέση ως εξής:
Γράφουμε την εξίσωση του Πυθαγόρα στη μορφή
(a/c)² + (b/c)² = 1
oπότε μπορούμε να την ερμηνεύσουμε λέγοντας ότι το σημείο (x,y) με x = (a/c) και y= (b/c), βρίσκεται πάνω στον μοναδιαίο κύκλο με εξίσωση
x² + y² = 1.
H θεωρία των τριγωνομετρικών συναρτήσεων παρέχει τότε έναν κομψό και απλό τρόπο παραμετροποίησης του κύκλου, έτσι ώστε να τον παραστήσουμε μέσω μιας μόνο βοηθητικής μεταβλητής. Η θεμελιώδης σχέση που συνδέει το ημίτονο και το συνημίτονο οποιασδήποτε γωνίας Α είναι:
συν²Α + ημ²Α = 1.
Τούτο σημαίνει πως αν θέσουμε x=συνΑ και y=ημΑ, τότε το σημείο με συντεταγμένες (x,y) βρίσκεται πάνω στον μοναδιαίο κύκλο. Για να συνοψίσουμε: η επίλυση της πυθαγόρειας εξίσωσης στο σύνολο των ακέραιων αριθμών ισοδυναμεί με την εύρεση μιας γωνίας Α, τέτοιας ώστε το συνΑ και το ημΑ να είναι ρητοί αριθμοί (αντίστοιχα ίσοι με a/c και b/c). Επειδή οι τριγωνομετρικές συναρτήσεις έχουν πολλών ειδών καλές ιδιότητες, τούτη η ιδέα είναι η βάση μιας πραγματικά γόνιμης θεωρίας για την εξίσωση του Πυθαγόρα.
Η εικασία του Taniyama δηλώνει ότι η ίδια τακτική μπορεί να ακολουθηθεί αν ο κύκλος αντικατασταθεί από μια ελλειπτική καμπύλη, αλλά με χρήση συναρτήσεων πιο εκλεπτυσμένων από τις τριγωνομετρικές, των ονομαζομένων “modular” συναρτήσεων. Ειδικότερα δηλώνει ότι κάθε ελλειπτική καμπύλη είναι δυνατόν να παραμετροποιηθεί μέσω κατάλληλων modular συναρτήσεων, όπως ακριβώς συμβαίνει για τον κύκλο μέσω του ημιτόνου και του συνημιτόνου.

Η ελλειπτική καμπύλη του Frey

Μεταξύ των ετών 1970 – 1975 o Υves Hellegouarch δημοσίευσε μια σειρά εργασιών που αφορούσαν τη σύνδεση των καμπυλών Fermat
xⁿ + yⁿ = zⁿ
και των ελλειπτικών καμπυλών• χρησιμοποίησε δε τις εργασίες αυτές για να συναγάγει θεωρήματα για τις ελλειπτικές καμπύλες, από γνωστά επιμέρους συμπεράσματα πάνω στο τελευταίο θεώρημα του Fermat.

O Jean-Pierre Serre πρότεινε τη χρήση της ιδέας με την αντίστροφη πορεία, δηλαδή την αναζήτηση ιδιοτήτων των ελλειπτικών καμπυλών για απόδειξη αποτελεσμάτων σχετικών με το τελευταίο θεώρημα του Fermat. Bρήκε στοιχεία που έδειχναν ότι η συγκεκριμένη αυτή γραμμή προσέγγισης είχε τη δυνατότητα να λύσει το πρόβλημα• κι έτσι οι ειδικοί άρχισαν να πιστεύουν πως το τελευταίο θεώρημα του Fermat βρισκόταν στην πορεία για να αποκαλύψει τα μυστικά του. Θα χρειαζόταν όμως μεγάλος τεχνικός αγώνας.

Το 1985, σε μια διάλεξη που δόθηκε στο διεθνές κέντρο μαθηματικών ερευνών στο Ομπερβόλφαχ, στον Μέλανα Δρυμό της Γερμανίας, ο Gerhard Frey συγκεκριμενοποίησε την πρόταση του Serre, εισάγοντας μια καμπύλη – γνωστή πλέον με το όνομα ελλειπτική καμπύλη του Frey – σε σχέση με την υποθετική λύση για το τελευταίο θεώρημα του Fermat.
H μορφή που επιλέχθηκε για την εν λόγω καμπύλη ανάγεται στον Hellegouarch, αλλά ο Frey σκόπευε να τη χρησιμοποιήσει με διαφορετικό τρόπο. Υποθέστε ότι υπάρχει μια μη τετριμμένη λύση
Αⁿ + Βⁿ = Cⁿ
για την εξίσωση του Fermat (δηλαδή τα Α, Β, C είναι όλα διάφορα του 0).
Διαλέγουμε αυτή την υποθετική λύση και στο εξής τα Α, Β, C θα συμβολίζουν σταθερούς (αλλά άγνωστους) μη μηδενικούς ακεραίους. Το μόνο γνωστό στοιχείο για τους A, B, C είναι ότι ικανοποιούν τη σχέση
Αⁿ + Βⁿ = Cⁿ
για n≥3, αν και μπορούμε να θέσουμε ένα επιπλέον στοιχείο, υποθέτοντας ότι οι Α, Β και C είναι μεταξύ τους πρώτοι.

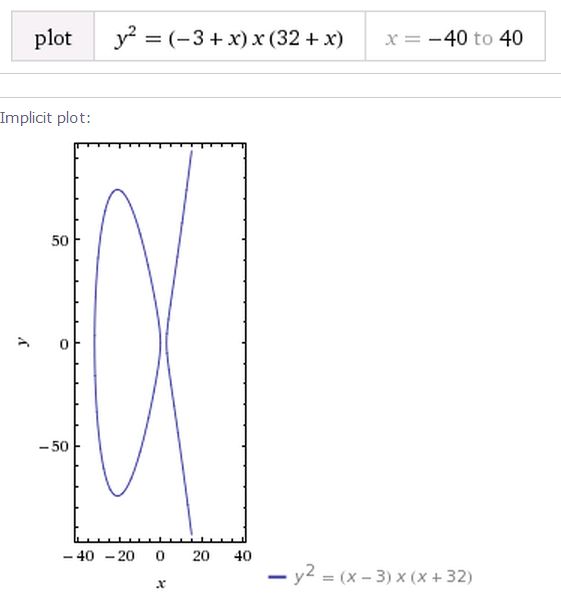
Ελλειπτική καμπύλη είναι ο γεωμετρικός τόπος των σημείων που ικανοποιούν μια συγκεκριμένη κυβική εξίσωση. Τέτοιου είδους καμπύλες βρίσκονται σε στενή κυβική εξίσωση. Τέτοιου είδους καμπύλες  βρίσκονται σε στενή σύνδεση με το τελευταίο θεώρημα του Fermat. Ειδικότερα, αν υπήρχε ένα αντιπαράδειγμα στο θεώρημα, θα συνεπαγόταν την ύπαρξη μιας ελλειπτικής καμπύλης με κάποιες πολύ ξεχωριστές ιδιότητες. Η καμπύλη που παρουσιάζεται εδώ, ορίζεται από την εξίσωση y² = x(x-3)(x+32)
www.wolframalpha.com

Τώρα θεωρείστε τη συγκεκριμένη (αλλά άγνωστη και πιθανώς ανύπαρκτη) ελλειπτική καμπύλη, με εξίσωση  y² = x(x+Aⁿ)(x-Bⁿ)
Πρόκειται για την ελλειπτική καμπύλη του Frey, και υπάρχει αν και μόνο αν το τελευταίο θεώρημα του Fermat δεν αληθεύει. Έτσι, αρκεί να δείξουμε ότι τούτη η καμπύλη δεν μπορεί να υπάρξει. Ο τρόπος για να επιτύχουμε το σκοπό μας είναι να υποθέσουμε αρχικά ότι η καμπύλη υπάρχει, και στη συνέχεια να καταλήξουμε σε κάποιο αντιφατικό συμπέρασμα.

Ο Frey είχε την ιδέα ότι, αν η καμπύλη του υπήρχε, τότε θα ήταν πραγματικά ένα πολύ παράξενο τέρας. Το 1986 ο Kenneth Ribet επαλήθευσε την ιδέα του Frey δεν είναι δυνατόν να παραμετροποιηθεί μέσω modular συναρτήσεων. Αν λοιπόν η εικασία του Taniyama αληθεύει, τότε ως απόρροια αληθεύει και το τελευταίο θεώρημα του Fermat.

Kάτι τέτοιο αποτελεί ουσιαστικής σημασίας κρίκο στην αλυσίδα Fermat, διότι δείχνει πως το τελευταίο θεώρημα του Fermat δεν είναι απλά ένα απομονωμένο αξιοπερίεργο, αλλά τοποθετείται στην καρδιά της σύγχρονης θεωρίας αριθμών.

Επτά χρόνια προσπαθειών

Από τα παιδικά του χρόνια ακόμη, ο Andrew Wiles επιθυμούσε να αποδείξει το τελευταίο θεώρημα του Fermat. Όταν όμως έγινε επαγγελματίας μαθηματικός, απέκτησε τη γνώμη πως επρόκειτο για ένα απομονωμένο και δύσκολο πρόβλημα – το οποίο θα ήταν όμορφο να αποδειχτεί αλλά όχι αντάξιο της φήμης του. κατόπιν έμαθε για την εργασία του Ribet και μετέβαλε ριζικά την άποψή του, αποφασίζοντας να αφιερώσει όλη του την ερευνητική εργασία για μια απόδειξη.

Γρήγορα αντελήφθη ότι δεν ήταν απαραίτητα η χρήση της εικασίας του Taniyama σε όλη της την έκταση, για μια ειδική περίπτωση, που καλύπτεται από την εικασία, συγκεκριμένα εκέινη που αφορά μια κατηγορία ελλειπτικών καμπυλών γνωστών ως «ημιευσταθών».
Ο Wiles «έσπασε» το πρόβλημα σε έξι κομμάτια, τα οποία έλυσε τμηματικά, μέχρι που τελικά μόνο ένα από αυτά του αντιστεκόταν σθεναρά. Και τότε, μια διάλεξη του Barry Mazur, με τελείως διαφορετικό αντικείμενο, του έδωσε μια ιδέα καθοριστικής σημασίας.
Σε μια εργασία του όγκου 200 σελίδων ο Wiles επιστράτευσε αρκετά ισχυρούς μηχανισμούς ώστε να δείξει πως η εικασία του Taniyama ίσχυε για τις ημιευσταθείς καμπύλες. Κάτι τέτοιο του ήταν αρκετό για να μπορέσει στη συνέχεια να αποδείξει το ακόλουθο θεώρημα:
Έστω Μ και Ν δυο άνισοι, μη μηδενικοί και πρώτοι μεταξύ των ακέραιοι, τέτοιοι ώστε ο αριθμός
Μ Ν (Μ – Ν)
να είναι διαιρετός δια 16. Τότε η ελλειπτική καμπύλη
y² = x(x+Μ)(x+Ν)
είναι δυνατόν να παραμετρικοποιηθεί μέσω modular συναρτήσεων. Πράγματι, η συνθήκη περί διαιρετότητας δια 16 υποδηλώνει ότι η παραπάνω καμπύλη είναι ημιευσταθής. Έτσι, η περίπτωση της εικασίας του Taniyama, που αφορά τις ημιευσταθείς καμπύλες, εδραιώνει την ύπαρξη της αναγκαίας ιδιότητας.

Ας εφαρμόσουμε τώρα το θεώρημα του Wiles στην καμπύλη του Frey, θέτοντας
Μ=Αⁿ και Ν=-Βⁿ.
Τότε Μ – Ν = Αⁿ + Βⁿ = Cⁿ,
οπότε
ΜΝ(Μ-Ν)=-ΑⁿΒⁿ Cⁿ,
και αρκεί να δείξουμε ότι το τελευταίο γινόμενο είναι πολλαπλάσιο του 16. Κάτι τέτοιο, όμως, είναι αρκετά απλό.
Τουλάχιστον ένας από τους Α, Β, C πρέπει να είναι άρτιος – αφού αν οι Α και Β είναι περιττοί, τότε ο Cⁿ ως άθροισμα δυο περιττών θα είναι άρτιος, πράγμα που σημαίνει ότι και ο C είναι άρτιος.
Μια κίνηση τακτικής μπορεί να μας διευκολύνει σοβαρά στην περαιτέρω πορεία: να θεωρήσουμε ότι n≥4, αντί του n≥3, μια και η απόδειξη του Euler καλύπτει την περίπτωση όπου n=3.
Παρατηρούμε τώρα ότι η τέταρτη ή οποιαδήποτε υψηλότερη δύναμη ενός άρτιου αριθμού είναι διαιρετή δια 2⁴=16, οπότε και το γινόμενο
-ΑⁿΒⁿ Cⁿ
είναι πολλαπλάσιο του 16.

Επομένως, η καμπύλη του Frey ικανοποιεί τις προϋποθέσεις του θεωρήματος του Wiles, γεγονός που συνεπάγεται τη δυνατότητα παραμετρικοποίησής της μέσω modular συναρτήσεων. Ο Frey όμως είχε ήδη αποδείξει πως κάτι τέτοιο είναι αδύνατον!

Ιδού λοιπόν, η αντίφαση που εξαρχής αναζητούσαμε. Το ονειρικό οικοδόμημα που κτίσαμε, υποθέτοντας την ύπαρξη μη τετριμμένης λύσης για την εξίσωση του Fermat – με n≥3 – κατέρρευσε. Έτσι αποδεικνύεται ότι μια τέτοια λύση δεν μπορεί να υπάρξει, και συνακολούθως το τελευταίο θεώρημα του Fermat είναι αληθές.

Συνοψίζοντας: η στρατηγική που ακολούθησε ο Wiles δείχνει την ορθότητα της εικασίας του Taniyama για ημιευσταθείς καμπύλες, κάτι που με τη σειρά του δείχνει πως το επιχείρημα του Ribet αποδεικνύει ότι η καμπύλη του Frey δν υπάρχει – και ο Fermat δικαιώνεται.

Ο Wiles είχε ένα ισχυρό οπλοστάσιο τεχνικών στη διάθεσή του, αλλά χρειάστηκαν επτά χρόνια εντατικής εργασίας για να συνθέσει μια απόδειξη. Ωστόσο, μόλις η αποδεικτική του διαδικασία κοινοποιήθηκε, ανέκυψαν ερωτήματα και αμφιβολίες για την ακεραιότητά της.
Τελικά. όμως, ο Mazur εξέφρασε την ομόφωνη παραδοχή του μαθηματικού κόσμου για την ορθότητα της μεθόδου.

Αναστάτωση τον όγδοο χρόνο

Η πλήρης παρουσίαση της εργασίας του Wiles ακολούθησε μιαν ασυνήθη οδό.
Δεν δημοσιεύθηκε ευρέως, αλλά υποβλήθηκε στο εγκυρότερο μαθηματικό περιοδικό, το Inventiones Mathematicae, μέσω του οποίου εστάλη σε έξι ειδικούς κριτές.
Στο μεταξύ, σταχυολογήματα τεχνικών λεπτομερειών της απόδειξης – από ανθρώπους που παρευρίσκονταν στο Ινστιτούτο Newton του Πανεπιστημίου του Καίμπριτζ κατά την ανακοίνωση του Wiles – έγιναν έναυσμα για τα πρώτα σχόλια, απορίες, ακόμη και αστεϊσμούς.

Ο Andrew Wiles: εάν είχατε λύσει ένα πρόβλημα 350 ετών, δεν θα χαμογελούσατε κι εσείς;

Ύστερα από μερικές εβδομάδες ενθουσιασμού, άρχισαν να διαρρέουν φήμες για κάποιο πιθανό λάθος. Στις 6 Δεκεμβρίου του 1993, ο Wiles έδωσε το δικό του μήνυμα μέσω ηλεκτρονικού ταχυδρομείου, στο οποίο ανέφερε, σε γενικές γραμμές, τα εξής: «τα όσα προβλήματα προέκυψαν κατά την κρίση της εργασίας, είχαν όλα επιλυθεί εκτός από ένα. Παρά το ότι η κύρια αναγωγή της εικασίας Taniyama στον υπολογισμό της ομάδας Selmer ήταν ορθή, ο τελικός υπολογισμός ενός επακριβούς άνω φράγματος για την εν λόγω ομάδα, στην ημιευσταθή περίπτωση, δεν ήταν ολοκληρωμένος».

Δεν παρέλειψε όμως να εκφράσει την αισιοδοξία του για τη σύντομη διευθέτηση της εναπομένουσας λεπτομέρειας. Παρ’ όλα αυτά, ο χρόνος κυλούσε χωρίς να συμμερίζεται την αισιοδοξία του Wiles.

Δικαίωση τον ένατο χρόνο

Το φθινόπωρο του 1994, πολλοί ειδικοί είχαν αρχίσει να απελπίζονται με την εκκρεμότητα της απόδειξης, εκτιμώντας ότι μια περίοδος τριών ακόμη ετών ήταν απαραίτητη για την κάλυψή της. Στις 26 Οκτωβρίου 1994, ένα μήνυμα από τον Rubin, τον μαθηματικό του Πολιτειακού Πανεπιστημίου του Οχάιο, ήρθε να μεταβάλλει εντελώς την κατάσταση. Το μήνυμα έλεγε τα εξής:
«Σήμερα το πρωί δημοσιεύτηκαν δυο χειρόγραφες εργασίες: οι ελλειπτικές καμπύλες και το τελευταίο θεώρημα του Fermat, από τον Andrew Wiles, και θεωρητικές ιδιότητες των δακτυλίων για ορισμένες άλγεβρες Hecke, από τους Richard Taylor και Αndrew Wiles.
Η πρώτη (εκτενής) αναγγέλλει – μεταξύ άλλων – μια απόδειξη του τελευταίου θεωρήματος του Fermat, στηριζόμενη, για ένα βασικό της βήμα, στην δεύτερη εργασία.
Όπως οι περισσότεροι γνωρίζετε, στην επιχειρηματολογία που παρουσιάστηκε από τον Wiles στις διαλέξεις του στο Καίμπριτζ προέκυψε ένα σοβαρό κενό – συγκεκριμένα η κατασκευή ενός συστήματος Euler.
Έπειτα από ανεπιτυχείς προσπάθειες, ο Wiles επιχείρησε εκ νέου μια διαφορετική προσέγγιση, την οποία, αν και είχε πρωτύτερα δοκιμάσει, την είχε εγκαταλείψει προς χάριν της ιδέας του συστήματος Εuler. Μπόρεσε έτσι να ολοκληρώσει την απόδειξή του, με την υπόθεση ότι ορισμένες άλγεβρες Hecke είναι τοπικές πλήρεις τομές. Η εν λόγω ιδέα, καθώς και οι υπόλοιπες που παρουσιάστηκαν στις διαλέξεις του Καίμπριτζ, αναγράφονται στο πρώτο χειρόγραφο. Οι Taylor και Wiles εδραιώνουν την απαραίτητη ιδιότητα που διαθέτουν οι άλγεβρες Hecke από κοινού στη δεύτερη εργασία».

Ως το 1995 οι δυο ανωτέρω εργασίες είχαν κριθεί, εγκριθεί και γίνει δεκτές για δημοσίευση. Το μυθιστόρημα του Fermat είχε φτάσει στο τέλος του, ή, ακριβέστερα, σε μια νέα αρχή.
Ήδη η απόδειξη απλοποιείται. Η νεώτερη επιχειρηματολογία του Wiles είναι συντομότερη σε έκταση και πολύ απλούστερη από την πρώτη ανολοκλήρωτη προσπάθεια. Λέγεται ότι ο αριθμοθεωρητικός του Πανεπιστημίου της Βόνης Faltings έχει ήδη απλουστεύσει κάποια τμήματά της. Το σημαντικότερο, έχουμε πλέον πρόσβαση σ’ ένα πλήθος από νέες ισχυρές τεχνικές – ειδικότερα, την ημιευσταθή περίπτωση της εικασίας του Taniyama – τις οποίες μπορούμε να εφαρμόσουμε σε άλλα ερωτήματα που αφορούν τις ελλειπτικές καμπύλες και οτιδήποτε συνδέεται με αυτές. Μια νέα δύναμη εμφανίζεται στην καρδιά της θεωρίας αριθμών.

Επίλογος

Διέθετε άραγε ο Fermat μια απόδειξη του θεωρήματός του; Eίναι εντελώς απίθανο να είχε κατά νου κάτι παρόμοιο με την απόδειξη που μας παρέδωσε ο Wiles. Πολλές μαθηματικές έννοιες μεγάλης σπουδαιότητας – όπως οι ελλειπτικές καμπύλες και οι modular συναρτήσεις – ήταν άγνωστες την εποχή του Fermat. H προσέγγιση του Wiles περιλαμβάνει μεγάλο μέρος της μοντέρνας αλγεβρικής θεωρίας αριθμών και της αλγεβρικής γεωμετρίας.
Η οπτική γωνία του 20ου αιώνα θα ήταν εντελώς ακατανόητη για τον 19ο αιώνα, πός μάλλον για τον 17ο.

Κάτι τέτοιο αφήνει δυο ενδεχόμενα. Είτε ο Fermat είχε κάνει λάθος, νομίζοντας πως διέθετε μιαν απόδειξη, ή η ιδέα του ήταν πολύ διαφορετική.

ΠΗΓΗ:  περιοδικό QUANTUM, Μάρτιος/Απρίλιος 1997, Τόμος 4/Τεύχος 2

 https://physicsgg.me/2013/04/12

ΖΗΝΩΝ  ΠΑΠΑΖΑΧΟΣ