Ο Lennart Van Hirtum, μαθηματικός στο Πανεπιστήμιο Paderborn στη Γερμανία, βρήκε τον ένατο αριθμό Dedekind, χρησιμοποιώντας τον υπερυπολογιστή Noctua 2 στο "Paderborn Center for Parallel Computing (PC2)" του Πανεπιστημίου του Paderborn στην Βόρεια Ρηνανία-Βεστφαλία της Γερμανίας. Οι μαθηματικοί τον έψαχναν επί 32 χρόνια. Κάθε αριθμός Dedekind αντιπροσωπεύει τον αριθμό των πιθανών διαμορφώσεων ενός συγκεκριμένου είδους λογικής πράξης true-false σε διαφορετικές χωρικές διαστάσεις. Ο αριθμός D(9), πού υπολογίστηκε τώρα, αντιπροσωπεύει εννέα διαστάσεις. Ο προηγούμενος γνωστός αριθμός στην «ακολουθία Dedekind», ο D(8), ο οποίος ακολουθεί τους ίδιους κανόνες για οκτώ διαστάσεις, είχε υπολογιστεί το 1991 χρησιμοποιώντας έναν Cray 2, τον ισχυρότερο υπερυπολογιστή της εποχής. Για τον υπολογισμό του 10ου αριθμού Dedekind: «Αν το κάναμε τώρα, θα απαιτούσε επεξεργαστική ισχύ ίση με τη συνολική ισχύ εξόδου του ήλιου».

ΓΙΑΤΙ ΣΤΑΜΑΤΗΣΑΝ ΑΠΟΤΟΜΑ ΟΛΟΙ - ΜΜΕ, ΜΗΤΣΟΤΑΚΗΣ, "ΣΥΝΤΑΓΜΑΤΟΛΟΓΟΙ" - ΝΑ ΑΣΧΟΛΟΥΝΤΑΙ ΜΕ ΤΟΥΣ "ΣΠΑΡΤΙΑΤΕΣ"; Ο Ιουδαίος επικοινωνιολόγος του Μητσοτάκη, Σταν Γκρίνμπεργκ, ουσιαστικά ο υπερπρωθυπουργός της χώρας, επέβαλε πλήρη σιγή: "ΜΑΣ ΤΗΝ ΕΦΕΡΕ Ο ΣΠΟΥΔΑΙΟΣ ΣΚΑΚΙΣΤΗΣ ΚΑΣΙΔΙΑΡΗΣ, ΘΑ ΤΟΥ ΤΗΝ ΦΕΡΟΥΜΕ ΚΙ ΕΜΕΙΣ. ΑΣ ΤΟΥΣ ΚΟΙΜΙΣΟΥΜΕ ΤΩΡΑ". ΚΑΠΟΙΟ ΠΡΩΙΝΟ ΘΑ ΣΥΓΚΛΗΘΕΙ ΤΟ "ΑΝΕΞΑΡΤΗΤΟ ΕΚΛΟΓΟΔΙΚΕΙΟ" ΑΠΟ "ΔΙΚΑΣΤΕΣ" ΤΥΠΟΥ ΚΛΑΠΑ, ΛΕΠΕΝΙΩΤΗ ΚΑΙ ΝΤΟΓΙΑΚΟΥ. ΘΑ ΚΗΡΥΞΕΙ ΕΚΠΤΩΤΟΥΣ ΤΟΥΣ ΒΟΥΛΕΥΤΕΣ ΤΩΝ "ΣΠΑΡΤΙΑΤΩΝ". ΘΑ ΔΩΣΕΙ ΤΙΣ ΕΔΡΕΣ ΤΟΥ ΚΟΜΜΑΤΟΣ: ΜΙΑ ΣΤΟΝ ΝΑΤΣΙΟ, ΜΙΑ ΣΤΟΝ ΒΕΛΟΠΟΥΛΟ, ΜΙΑ ΣΤΗΝ ΚΩΝΣΤΑΝΤΟΠΟΥΛΟΥ, ΜΙΑ ΣΤΟΝ ΚΟΥΤΣΟΥΜΠΑ, ΔΥΟ ΣΤΟ ΚΛΕΦΤΟΠΑΣΟΚ, ΔΥΟ ΣΤΟ ΣΥΡΙΖΑ ΚΑΙ ΤΕΣΣΕΡΙΣ ΣΤΗΝ ΟΙΚΟΓΕΝΕΙΑ ΜΗΤΣΟΤΑΚΗ. Όλοι θα είναι ευχαριστημένοι. Την άλλη μέρα το θέμα θα κλείσει απότομα με πλήρη σιγή και κανείς δεν θα ξανααναφερθεί σ'αυτό. Έτσι τακτοποιούνται οι υποθέσεις σε μια Μπανανία του Κορλεόνε.

ΣΤΙΣ ΤΕΛΕΥΤΑΙΕΣ ΘΕΣΕΙΣ ΠΑΓΚΟΣΜΙΩΣ ΤΑ ΕΛΛΗΝΙΚΑ ΠΑΝΕΠΙΣΤΗΜΙΑ. ΤΟ ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΕΙΝΑΙ ΤΕΛΕΥΤΑΙΟ ΣΤΗΝ 1400ή.Το Εθνικό Μετσόβιο Πολυτεχνείο το 1973 ήταν ανάμεσα στα 30 καλύτερα Πανεπιστήμια του κόσμου. Ο καθηγητής και πρύτανις του Εθνικού Μετσόβιου Πολυτεχνείου, Ιωάννης Θεοφανόπουλος το 1932 ανέλαβε διευθυντής του μηχανουργικού εργοστασίου-εργαστηρίου της Σχολής, προώθησε την κατασκευή του πρώτου τετράχρονου κινητήρα Diesel στη Σχολή, ισχύος 5 ίππων, και πρωτοστάτησε στην επέκταση του Μηχανουργείου στην οδό Τοσίτσα. Βασικό του έργο θεωρούνται τα «Στοιχεία Μηχανών και Εμβολοφόρων Αντλιών». Το 2023, σε 50 χρόνια, οι "έλληνες πολιτικοί" και οι κομμουνιστές έφεραν το Πολυτεχνείο στην 347η θέση.

                                               

Ο Ιούλιος Βίλχελμ Ρίχαρντ Ντέντεκιντ ήταν Γερμανός μαθηματικός που συνεισέφερε σημαντικά στη θεωρία των αριθμών, στην αφηρημένη άλγεβρα και στις αξιωματικές βάσεις της αριθμητικής. Η πιο γνωστή συνεισφορά του είναι ο ορισμός των πραγματικών αριθμών μέσω της έννοιας της τομής Ντέντεκιντ.

 Οι ερευνητές υπολόγισαν τον «ένατο αριθμό Dedekind», ο οποίος ανήκει σε μια εκθετικά σύνθετη σειρά αριθμών που ορίζουν εξόδους λογικών συναρτήσεων με βάση διαφορετικές χωρικές διαστάσεις.

Μαθηματικοί οπλισμένοι με υπερυπολογιστές εντόπισαν επιτέλους την αξία ενός μεγάλου αριθμού που προηγουμένως θεωρούνταν αδύνατο να υπολογιστεί.

 

Φωτογραφία από Nothing Ahead: https://www.pexels.com/el-gr/photo/3729557/

Όπως καταγράφει ο  Χάρι Μπέικερ στο Live Science

Ο αριθμός, γνωστός ως “ένατος αριθμός Dedekind” ή D(9), είναι στην πραγματικότητα ο 10ος σε μια ακολουθία. Κάθε αριθμός Dedekind αντιπροσωπεύει τον αριθμό των πιθανών διαμορφώσεων ενός συγκεκριμένου είδους λογικής πράξης true-false σε διαφορετικές χωρικές διαστάσεις.

(Ο πρώτος αριθμός στην ακολουθία είναι D(0), που αντιπροσωπεύει μηδενικές διαστάσεις. Γι’ αυτό το D(9), που αντιπροσωπεύει εννέα διαστάσεις, είναι ο 10ος αριθμός στην ακολουθία.)

Οι αριθμοί Dedekind γίνονται ολοένα και μεγαλύτεροι για κάθε νέα διάσταση, γεγονός που καθιστά όλο και πιο δύσκολο τον προσδιορισμό τους.

Ο όγδοος αριθμός Dedekind, ο οποίος ακολουθεί τους ίδιους κανόνες για οκτώ διαστάσεις, υπολογίστηκε το 1991. Αλλά λόγω του άλματος στην υπολογιστική ισχύ που απαιτείται για τον υπολογισμό της ένατης, ορισμένοι μαθηματικοί θεώρησαν ότι ήταν αδύνατο να υπολογίσουν την ακριβή τιμή του.

Αλλά τώρα, δύο άσχετες μελέτες από ξεχωριστές ερευνητικές ομάδες – η πρώτη που υποβλήθηκε στον διακομιστή προεκτύπωσης arXiv στις 5 Απριλίου και η δεύτερη στον ίδιο διακομιστή στις 6 Απριλίου – έχουν κάνει το αδύνατο. Οι μελέτες -η καθεμία χρησιμοποιώντας έναν υπερυπολογιστή αλλά εκτελούσε διαφορετικά προγράμματα- παρήγαγαν τον ίδιο ακριβώς αριθμό.

Τα αποτελέσματα δεν έχουν ακόμη αξιολογηθεί από ομοτίμους. Αλλά επειδή οι μελέτες κατέληξαν στο ίδιο συμπέρασμα, είναι «100% βέβαιο» ότι ο αριθμός έχει αποκρυπτογραφηθεί σωστά, ο κύριος συγγραφέας στη δεύτερη εργασία, Lennart Van Hirtum, μαθηματικός στο Πανεπιστήμιο Paderborn στη Γερμανία και κύριος συγγραφέας στη δεύτερη εργασία, είπε στο Live Science.

Ο Van Hirtum και οι συνεργάτες του υπερασπίστηκαν το έργο τους κατά τη διάρκεια μιας διάλεξης στο Πανεπιστήμιο Paderborn στις 27 Ιουνίου.

Τι είναι οι αριθμοί Dedekind;

Οι αριθμοί Dedekind περιγράφηκαν για πρώτη φορά από τον Γερμανό μαθηματικό Richard Dedekind τον 19ο αιώνα. Οι αριθμοί σχετίζονται με λογικά προβλήματα γνωστά ως “μονότονες δυαδικές συναρτήσεις” (MBFs).

Οι συναρτήσεις Boolean είναι ένα είδος λογικής που μπορεί να λάβει ως είσοδο μόνο μία από τις δύο τιμές -0 (false) και 1 (true)- και να ξεχωρίσει μόνο αυτές τις δύο τιμές.

Στα MBF μπορείτε να αλλάξετε το 0 με ένα 1 στην είσοδο, αλλά μόνο εάν επιτρέπει στην έξοδο να αλλάξει από 0 σε 1, όχι από 1 σε 0.

Οι αριθμοί Dedekind είναι η έξοδος των MBF όπου η είσοδος είναι συγκεκριμένη χωρική διάσταση.

Αυτή η έννοια μπορεί να προκαλέσει σύγχυση για τους μη μαθηματικούς. Αλλά είναι δυνατό να οπτικοποιήσουμε τι συμβαίνει χρησιμοποιώντας σχήματα για να αναπαραστήσουμε τους αριθμούς Dedekind για κάθε διάσταση, εξήγησε ο Van Hirtum.

Για παράδειγμα, στη δεύτερη διάσταση, ο αριθμός Dedekind σχετίζεται με ένα τετράγωνο, ενώ ο τρίτος μπορεί να αναπαρασταθεί με έναν κύβο, ο τέταρτος και μεγαλύτερος με υπερκύβους.

Για κάθε διάσταση, οι κορυφές ή τα σημεία ενός συγκεκριμένου σχήματος αντιπροσωπεύουν τις πιθανές διαμορφώσεις των MBF (βλ. εικόνα παρακάτω).

Για να βρείτε τον αριθμό Dedekind, μπορείτε να μετρήσετε πόσες φορές μπορείτε να χρωματίσετε κάθε κορυφή από κάθε σχήμα με ένα από τα δύο χρώματα (σε αυτήν την περίπτωση κόκκινο και λευκό), αλλά με την προϋπόθεση ότι δεν μπορεί να τοποθετηθεί ένα χρώμα (σε αυτήν την περίπτωση το λευκό). πάνω από το άλλο (σε αυτή την περίπτωση κόκκινο).

Ένα διάγραμμα που δείχνει τις πιθανές διαμορφώσεις των έγχρωμων κορυφών μέσα σε όλο και πιο πολύπλοκα σχήματα

Ένα διάγραμμα που δείχνει τις εξόδους για τους τέσσερις πρώτους αριθμούς Dedekind: Από αριστερά προς τα δεξιά D(0), D(1), D(2) και D(3). Οι κύκλοι αντιπροσωπεύουν μια πιθανή διαμόρφωση για κάθε σχήμα όπου οι λευκές κορυφές δεν τοποθετούνται πάνω από τις κόκκινες. (Εικόνα: Πανεπιστήμιο Paderborn)

Για μηδενικές διαστάσεις, το σχήμα είναι μόνο ένα σημείο και D(0)=2 επειδή το σημείο μπορεί να είναι είτε κόκκινο είτε λευκό. Για μια διάσταση, το σχήμα είναι μια γραμμή με δύο σημεία και D(1)=3 επειδή και τα δύο σημεία μπορεί να είναι είτε το ίδιο χρώμα είτε κόκκινα πάνω από το λευκό.

Για δύο διαστάσεις, το σχήμα είναι τετράγωνο και D(2)=6 επειδή υπάρχουν πλέον έξι πιθανά σενάρια όπου καμία λευκή κουκκίδα δεν βρίσκεται πάνω από μια κόκκινη κουκκίδα. Και για τις τρεις διαστάσεις, το σχήμα είναι ένας κύβος, και ο αριθμός των πιθανών διαμορφώσεων μεταβαίνει σε 20, άρα D(3)=20.

Καθώς ο αριθμός των διαστάσεων αυξάνεται, το υποθετικό σχήμα γίνεται ένας όλο και πιο πολύπλοκος υπερκύβος με μεγαλύτερο αριθμό αποτελεσμάτων, είπε ο Van Hirtum.

Οι τιμές των επόμενων πέντε αριθμών Dedekind είναι 68, 7581, 7828354, 2414682040998 και 56130437228687557907788.

Η τιμή που προσδιορίστηκε πρόσφατα για το D(9) είναι 286386577668298411128469151667598498812366.

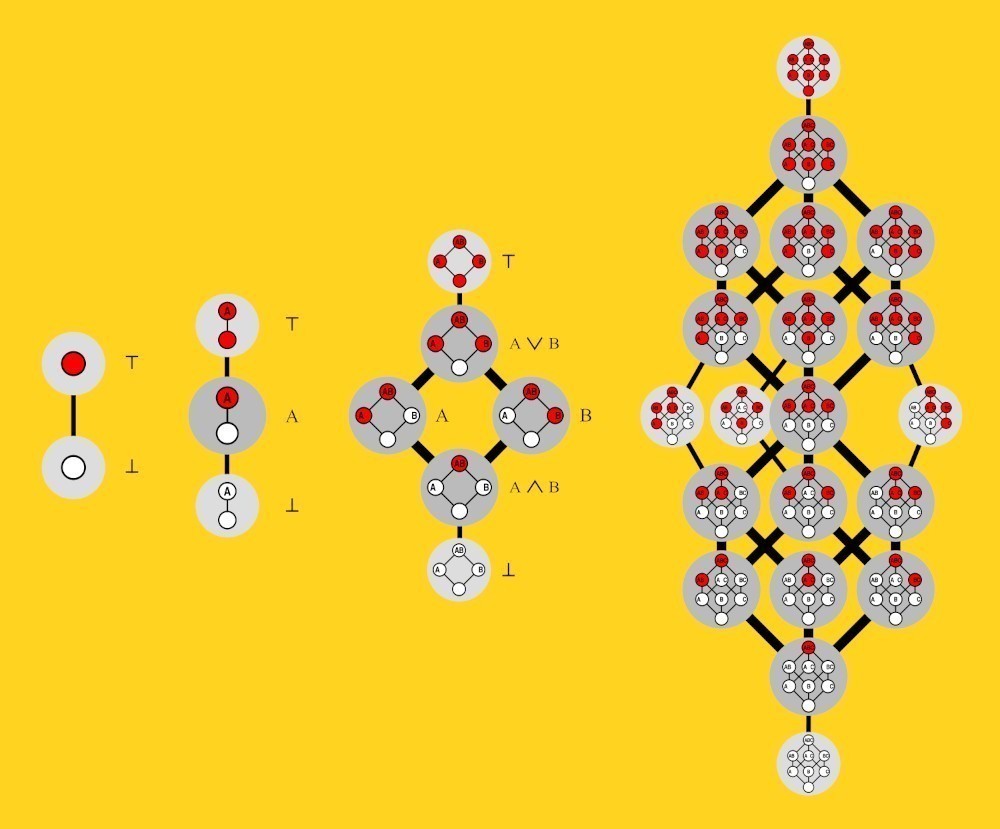
Όλο και πιο περίπλοκοι υπολογισμοί

Ο Van Hirtum εργάζεται για τον εντοπισμό του D(9) για περισσότερα από τρία χρόνια. Για να το κάνει αυτό, δημιούργησε ένα νέο είδος προγράμματος υπολογιστή για να επιτρέψει σε έναν υπερυπολογιστή να επεξεργάζεται τα δεδομένα με συγκεκριμένο τρόπο.

Εάν είχε χρησιμοποιήσει ένα πιο βασικό πρόγραμμα, θα μπορούσαν να χρειαστούν έως και 100 χρόνια για να ολοκληρωθούν οι υπολογισμοί, ακόμη και με ένα προηγμένο μηχάνημα που τσακίζει τους αριθμούς, είπε.

Αφού δημιούργησε τον κώδικα του υπολογιστή του, η ομάδα του Van Hirtum πέρασε περισσότερους από τέσσερις μήνες χρησιμοποιώντας τον υπερυπολογιστή στο Πανεπιστήμιο του Leuven στο Βέλγιο για να επεξεργαστεί τα δεδομένα.

Ωστόσο, οι υπολογισμοί δεν άργησαν πραγματικά να ολοκληρωθούν: Η φύση του προγράμματος σήμαινε ότι ήταν επιρρεπής σε λάθη εν μέρει, πράγμα που σήμαινε ότι η ομάδα έπρεπε να επανεκκινεί συνεχώς την εργασία, είπε ο Van Hirtum.

Συγκριτικά, ο υπολογιστής που χρησιμοποιήθηκε το 1991 για την επεξεργασία του D(8) ήταν λιγότερο ισχυρός από ένα σύγχρονο smartphone και ολοκλήρωσε την εργασία σε περίπου 200 ώρες. Ένας σύγχρονος φορητός υπολογιστής θα μπορούσε πιθανώς να εκτελέσει αυτούς τους υπολογισμούς σε λιγότερο από 10 λεπτά, είπε ο Van Hirtum.

Ο Van Hirtum πιστεύει ότι ένα παρόμοιο άλμα στην επεξεργαστική ισχύ του υπολογιστή θα απαιτηθεί για τον υπολογισμό του 10ου αριθμού Dedekind. «Αν το κάναμε τώρα, θα απαιτούσε επεξεργαστική ισχύ ίση με τη συνολική ισχύ εξόδου του ήλιου», είπε, γεγονός που καθιστά «πρακτικά αδύνατο» τον υπολογισμό.

Οι απαιτήσεις επεξεργαστικής ισχύος θα μπορούσαν να μειωθούν χρησιμοποιώντας πιο σύνθετους αλγόριθμους, είπε ο Van Hirtum.

«Αλλά έχουμε κάπως χτυπήσει έναν τοίχο με το πόσο πολύπλοκοι μπορούν να γίνουν οι αλγόριθμοι», πρόσθεσε.

Ωστόσο, άλλοι μαθηματικοί εξακολουθούν να ελπίζουν ότι το D(10) θα μπορούσε τελικά να υπολογιστεί, είπε ο Van Hirtum.

Πηγή Live Science

D(9) - Υπολογίστηκε ο ένατος αριθμός Dedekind

D(9) - Υπολογίστηκε ο ένατος αριθμός Dedekind | Άπειρο (apeiro.gr)

Οι ερευνητές του Πανεπιστημίου του Paderborn και του KU Leuven βρήκαν τη λύση σε μια μαθηματική πρόκληση που κρατούσε δεκαετίες υπολογίζοντας τον ένατο αριθμό Dedekind ή D(9), έναν απίστευτα τεράστιο αριθμό με 42 ψηφία, με τη βοήθεια ενός υπερυπολογιστή. Οι μαθηματικοί -και όχι μόνο- αναζητούσαν την ακριβή τιμή αυτού του αριθμού από το 1991.

Οι προηγούμενοι αριθμοί της σειράς είχαν βρεθεί από τον ίδιο τον μεγάλο μαθηματικό Richard Dedekind, όταν όρισε το πρόβλημα το 1897, και αργότερα από πρωτοπόρους της επιστήμης των υπολογιστών. Ο προηγούμενος γνωστός αριθμός στην «ακολουθία Dedekind», ο D(8) είχε υπολογιστεί το 1991 χρησιμοποιώντας έναν Cray 2, τον ισχυρότερο υπερυπολογιστή της εποχής. Από τότε και για 32 χρόνια, ο υπολογισμός του επόμενου αριθμού, του D(9), ήταν μια ανοιχτή πρόκληση. Αυτό ήταν το κίνητρο για το φιλόδοξο σχέδιο του Lennart Van Hirtum, τότε φοιτητή πληροφορικής στο KU Leuven και τώρα ερευνητή στο Πανεπιστήμιο του Paderborn, ο οποίος υπολόγισε τον D(9).

Κόκκοι άμμου, σκάκι και υπερυπολογιστές

Το κύριο αντικείμενο των αριθμών Dedekind είναι οι λεγόμενες μονότονες συναρτήσεις Boolean. Mπορείτε να σκεφτείτε μια μονότονη συνάρτηση Boolean σε δύο, τρεις και άπειρες διαστάσεις ως ένα παιχνίδι με έναν κύβο n διαστάσεων. Ισορροπείτε τον κύβο σε μια γωνία και στη συνέχεια χρωματίζετε κάθε μια από τις υπόλοιπες γωνίες είτε με λευκό είτε με κόκκινο χρώμα. Υπάρχει μόνο ένας κανόνας: δεν πρέπει ποτέ να τοποθετήσετε μια λευκή γωνία πάνω από μια κόκκινη. Αυτό δημιουργεί ένα είδος κάθετης διασταύρωσης κόκκινου-λευκού. Σκοπός του παιχνιδιού είναι να μετρήσετε πόσες διαφορετικές διασταυρώσεις υπάρχουν. Ο αριθμός τους ορίζεται ως ο αριθμός Dedekind. Μπορεί να μην το καταλαβαίνετε αμέσως, αλλά το μέγεθος των αριθμών γρήγορα απογειώνεται: ο 8ος αριθμός Dedekind έχει ήδη 23 ψηφία!

Τόσο μεγάλοι αριθμοί είναι γνωστοί από έναν θρύλο σχετικά με την εφεύρεση του παιχνιδιού του σκακιού. Σύμφωνα με αυτόν τον μύθο, ο εφευρέτης του σκακιού ζήτησε από τον βασιλιά μόνο μερικούς κόκκους ρυζιού σε κάθε τετράγωνο της σκακιέρας ως ανταμοιβή: έναν κόκκο στο πρώτο τετράγωνο, δύο κόκκους στο δεύτερο, τέσσερις στο τρίτο και διπλάσιους σε κάθε ένα από τα επόμενα τετράγωνα. Ο βασιλιάς κατάλαβε γρήγορα ότι το αίτημα αυτό ήταν αδύνατο να ικανοποιηθεί, επειδή τόσο πολύ ρύζι δεν υπάρχει σε ολόκληρο τον κόσμο! Ακόμα κι αν μπορούσε ο βασιλιάς να γεμίσει όλη τη σκακιέρα με ρύζι, ο αριθμός των συνολικών κόκκων ρυζιού θα είχε περίπου 20 ψηφία - ένα ασύλληπτο ποσό, αλλά και πάλι μικρότερο από το D(8)! Οπότε, με τέτοιες τάξεις μεγέθους, είναι προφανές ότι για την εύρεση του D(9) θα χρειαζόταν τόσο μια αποτελεσματική υπολογιστική μέθοδος όσο και ένας υπερυπολογιστής.

Ορόσημο: Τα χρόνια γίνονται μήνες

Για τον υπολογισμό του D(9), οι επιστήμονες χρησιμοποίησαν μια τεχνική που ανέπτυξε ο Patrick De Causmaecker, γνωστή ως τύπος του συντελεστή P (P-coefficient formula). Παρέχει έναν τρόπο υπολογισμού των αριθμών Dedekind όχι με μέτρηση, αλλά με ένα πολύ μεγάλο άθροισμα. Αυτό επιτρέπει την αποκωδικοποίηση του D(8) σε μόλις οκτώ λεπτά σε έναν κανονικό φορητό υπολογιστή. Αλλά, αυτό που διαρκεί οκτώ λεπτά για το D(8) γίνεται εκατοντάδες χιλιάδες χρόνια για το D(9). "Ακόμα και αν χρησιμοποιούσατε έναν μεγάλο υπερυπολογιστή αποκλειστικά για αυτό το έργο, θα χρειαζόταν πολλά χρόνια για να ολοκληρωθεί ο υπολογισμός", επισημαίνει ο Van Hirtum.

Το κύριο πρόβλημα είναι ότι ο αριθμός των όρων σε αυτόν τον τύπο αυξάνεται απίστευτα γρήγορα. «Στην περίπτωσή μας, εκμεταλλευόμενοι τις συμμετρίες στον τύπο, καταφέραμε να μειώσουμε τον αριθμό των όρων σε "μόνο" 5.5⋅1018$5.5\cdot {10}^{18}$. Συγκριτικά, ο αριθμός των κόκκων άμμου στη Γη είναι περίπου 7.5⋅1018$7.5\cdot {10}^{18}$, αλλά για έναν σύγχρονο υπερυπολογιστή, 5.5⋅1018$5.5\cdot {10}^{18}$ πράξεις είναι διαχειρίσιμες».

Το πρόβλημα: Ο υπολογισμός αυτών των όρων σε κανονικούς επεξεργαστές είναι αργός και ακόμα και η χρήση των GPUs, που είναι σήμερα η ταχύτερη τεχνολογία επιτάχυνσης υλικού για πολλές εφαρμογές τεχνητής νοημοσύνης, δεν είναι αποτελεσματική για αυτόν τον αλγόριθμο.

Η λύση: Υλικό ειδικά σχεδιασμένο για τη συγκεκριμένη εφαρμογή που χρησιμοποιεί εξειδικευμένες και παράλληλες αριθμητικές μονάδες, τις λεγόμενες FPGA (field programmable gate arrays). Ο Van Hirtum ανέπτυξε ένα αρχικό πρωτότυπο για τον επιταχυντή υλικού και άρχισε να αναζητά έναν υπερυπολογιστή που διέθετε τις απαραίτητες κάρτες FPGA. Αυτό ήταν ο Noctua 2 στο "Paderborn Center for Parallel Computing (PC2)" του Πανεπιστημίου του Paderborn, ο οποίος διαθέτει ένα από τα ισχυρότερα συστήματα FPGA στον κόσμο. Μετά από αρκετά χρόνια ανάπτυξης, το πρόγραμμα έτρεξε στον υπερυπολογιστή για περίπου. 

Και επιτέλους ήρθε η ώρα. Στις 8 Μαρτίου, το πρόγραμμα υπολόγισε τον 9ο αριθμό Dedekind, ο οποίος είναι ο

286386577668298411128469151667598498812366

Ρίχαρντ Ντέντεκιντ  (ΒΙΚΙΠΑΙΔΕΙΑ)

Ο Γιούλιους Βίλχελμ Ρίχαρντ Ντέντεκιντ (6 Οκτωβρίου 1831 - 12 Φεβρουαρίου 1916) ήταν Γερμανός μαθηματικός που συνεισέφερε σημαντικά στη θεωρία των αριθμών, στην αφηρημένη άλγεβρα (ιδίως στη θεωρία δακτυλίων) και στις αξιωματικές βάσεις της αριθμητικής. Η πιο γνωστή συνεισφορά του είναι ο ορισμός των πραγματικών αριθμών μέσω της έννοιας της τομής Ντέντεκιντ. Θεωρείται επίσης πρωτοπόρος στην ανάπτυξη της σύγχρονης θεωρίας συνόλων και της φιλοσοφίας των μαθηματικών που είναι γνωστή ως λογικισμός.^[12]

Βιογραφία[Επεξεργασία | επεξεργασία κώδικα]

Ο πατέρας του Ντέντεκιντ ήταν ο Γιούλιους Λέβιν Ούλριχ Ντέντεκιντ, διαχειριστής του Κολλεγίου Carolinum στο Μπράουνσβαϊγκ. Η μητέρα του ήταν η Καρολίν Χενριέτ Ντέντεκιντ ("γεννημένη Emperius"), κόρη ενός καθηγητή του Κολλεγίου^[13]. Ο Ρίτσαρντ Ντέντεκιντ είχε τρία μεγαλύτερα αδέλφια. Ως ενήλικας, δεν χρησιμοποίησε ποτέ το όνομα Γιούλιους Βίλχελμ. Γεννήθηκε στο Μπράουνσβαϊγκ, όπου έζησε το μεγαλύτερο μέρος της ζωής του και πέθανε.

Παρακολούθησε για πρώτη φορά το Κολλέγιο Carolinum το 1848, προτού εισαχθεί στο Πανεπιστήμιο του Γκέτινγκεν το 1850. Εκεί ο καθηγητής Μόριτς Στερν του δίδαξε τη θεωρία των αριθμών. Ο Γκάους εξακολουθούσε να διδάσκει, αλλά κυρίως σε στοιχειώδες επίπεδο, και ο Ντέντεκιντ ήταν ο τελευταίος του μαθητής. Ο Ντέντεκιντ έλαβε το διδακτορικό του το 1852,^[12] για μια διατριβή με τίτλο Über die Theorie der Eulerschen Integrale ("Για τη θεωρία των ολοκληρωμάτων του Όιλερ"). Η διατριβή αυτή δεν ήταν ενδεικτική του ταλέντου που θα έδειχνε ο Ντέντεκιντ στις μετέπειτα δημοσιεύσεις του.

Εκείνη την εποχή, το Πανεπιστήμιο του Βερολίνου, και όχι το Γκέτινγκεν, ήταν το κύριο κέντρο της μαθηματικής έρευνας στη Γερμανία. Επομένως, ο Ντέντεκιντ πήγε στο Βερολίνο για διετείς σπουδές, όπου ήταν σύγχρονοι με τον Μπέρνχαρντ Ρίμαν- και οι δύο έλαβαν το δίπλωμά τους το 1854. Ο Ντέντεκιντ επέστρεψε στο Γκέτινγκεν για να διδάξει ως Privatdozent, δίνοντας διαλέξεις για τις πιθανότητες και τη γεωμετρία. Σπούδασε για ένα διάστημα με τον Πέτερ Γκούσταβ Λεζέν Ντιριχλέ, με τον οποίο έγινε φίλος. Λόγω επίμονων αδυναμιών στις μαθηματικές του γνώσεις, μελέτησε ελλειπτικές και αβελιανές συναρτήσεις. Ήταν όμως και ο πρώτος στο Γκέτινγκεν που έδωσε διαλέξεις για τη θεωρία Γκαλουά. Παράλληλα, ήταν από τους πρώτους που κατανόησαν τη σημασία της έννοιας της ομάδας για την άλγεβρα και την αριθμητική.

Το 1858 άρχισε να διδάσκει στο Πολυτεχνείο της Ζυρίχης (σήμερα ETH Ζυρίχης). Όταν το Κολλέγιο Carolinum αναβαθμίστηκε σε Τεχνικό Ινστιτούτο ("Τεχνική Ανώτατη Σχολή") το 1862, ο Ντέντεκιντ επέστρεψε στη γενέτειρά του, το Μπράουνσβαϊγκ, όπου πέρασε το υπόλοιπο της ζωής του, διδάσκοντας στο Ινστιτούτο. Συνταξιοδοτήθηκε το 1894, αλλά δίδασκε περιστασιακά και συνέχισε να δημοσιεύει. Δεν παντρεύτηκε ποτέ, αλλά ζούσε με την αδελφή του Τζούλια.

Ο Ντέντεκιντ εξελέγη στις Ακαδημίες του Βερολίνου (1880) και της Ρώμης και στη Γαλλική Ακαδημία Επιστημών (1900). Έλαβε τιμητικούς διδακτορικούς τίτλους από τα πανεπιστήμια του Όσλο, της Ζυρίχης και του Μπραουνσβάιγκ.

Εργασίες[Επεξεργασία | επεξεργασία κώδικα]

Ενώ δίδασκε για πρώτη φορά λογισμό στην Πολυτεχνική Σχολή, ο Ντέντεκιντ ανέπτυξε την έννοια που σήμερα είναι γνωστή ως το κόψιμο Ντέντεκιντ (γερμανικά: Schnitt), το οποίο έχει γίνει ένας τυπικός ορισμός των πραγματικών αριθμών. Η ιδέα της τομής είναι ότι ένας άρρητος αριθμός διαιρεί τους ρητούς αριθμούς σε δύο κατηγορίες (σύνολα), με όλους τους αριθμούς της μιας (ανώτερης) κατηγορίας να είναι αυστηρά μεγαλύτεροι από όλους τους αριθμούς της άλλης (κατώτερης) κατηγορίας. Για παράδειγμα, η τετραγωνική ρίζα του 2 ορίζει όλους τους μη αρνητικούς αριθμούς των οποίων τα τετράγωνα είναι μικρότερα του 2 και τους αρνητικούς αριθμούς στην κατώτερη τάξη, και τους θετικούς αριθμούς των οποίων τα τετράγωνα είναι μεγαλύτερα του 2 στην ανώτερη τάξη. Κάθε θέση στη συνέχεια της αριθμογραμμής περιέχει είτε έναν ορθολογικό είτε έναν ανορθολογικό αριθμό. Επομένως, δεν υπάρχουν κενά, κενά ή ασυνέχειες. Ο Dedekind δημοσίευσε τις σκέψεις του σχετικά με τους άρρητους αριθμούς και τις περικοπές του Dedekind στο φυλλάδιο "Stetigkeit und irrationale Zahlen" ("Συνέχεια και άρρητοι αριθμοί")-^[14] στη σύγχρονη ορολογία, Vollständigkeit, πληρότητα.^[15]

Ο Ντέντεκιντ όρισε δύο σύνολα ως "όμοια" όταν υπάρχει μια αντιστοιχία ένα προς ένα μεταξύ τους^[16] Επικαλέστηκε την ομοιότητα για να δώσει τον πρώτο[παραπομπή απαιτείται] ακριβή ορισμό ενός άπειρου συνόλου: ένα σύνολο είναι άπειρο όταν είναι "όμοιο με ένα κατάλληλο μέρος του εαυτού του"^[17], στη σύγχρονη ορολογία, ισοδυναμεί με ένα από τα κατάλληλα υποσύνολά του. Μπορούμε επομένως να δείξουμε ότι το σύνολο N των φυσικών αριθμών είναι παρόμοιο με το υποσύνολο του N του οποίου τα μέλη είναι τα τετράγωνα κάθε μέλους του N²):

N    1  2  3  4  5  6  7  8  9  10 ...
             ↓           
N2   1  4  9  16 25 36 49 64 81 100 ...

Το έργο του Ντέντεκιντ σε αυτόν τον τομέα προηγήθηκε του έργου του Γκέοργκ Κάντορ, ο οποίος θεωρείται γενικά ο θεμελιωτής της θεωρίας συνόλων. Παρομοίως, η συμβολή του στα θεμέλια των μαθηματικών πρόλαβε το μεταγενέστερο έργο των κύριων υποστηρικτών του λογικισμού, όπως ο Γκότλομπ Φρέγκε και ο Μπέρτραντ Ράσελ.

Ο Ντέντεκιντ επιμελήθηκε τα συγκεντρωτικά έργα των Λεζέν Ντίριχλετ, Γκάους και Ρίμαν. Η μελέτη του έργου του Λεζέν Ντίριχλετ οδήγησε τον Ντέντεκιντ στη μετέπειτα μελέτη των αλγεβρικών αριθμητικών πεδίων και των ιδεωδών. Το 1863 δημοσίευσε τις διαλέξεις του Λεζέν Ντίριχλετ για τη θεωρία των αριθμών υπό τον τίτλο Vorlesungen über Zahlentheorie ("Διαλέξεις για τη θεωρία των αριθμών") :

Παρόλο που το βιβλίο βασίζεται σίγουρα στις διαλέξεις του Ντίριχλετ, και παρόλο που ο ίδιος ο Ντέντεκιντ αναφερόταν στο βιβλίο καθ' όλη τη διάρκεια της ζωής του ως βιβλίο του Ντίριχλετ, το ίδιο το βιβλίο γράφτηκε εξ ολοκλήρου από τον Ντέντεκιντ, σε μεγάλο βαθμό μετά το θάνατο του Ντίριχλετ.

Edwards, 1983

Οι εκδόσεις Vorlesungen του 1879 και του 1894 περιλάμβαναν συμπληρώματα που εισήγαγαν την έννοια του ιδανικού, η οποία είναι θεμελιώδης για τη θεωρία των δακτυλίων (η λέξη "δακτύλιος", που εισήγαγε αργότερα ο Χίλμπερτ, δεν εμφανίζεται στο έργο του Ντέντεκιντ). Ο Ντέντεκιντ ορίζει ένα ιδανικό ως ένα υποσύνολο ενός συνόλου αριθμών, το οποίο αποτελείται από αλγεβρικούς ακέραιους αριθμούς που ικανοποιούν πολυωνυμικές εξισώσεις με ακέραιους συντελεστές. Η έννοια αναπτύχθηκε από τον Χίλμπερτ και κυρίως από την Έμυ Νέτερ. Τα ιδανικά γενικεύουν τους ιδανικούς αριθμούς του Ερνστ Έντουαρντ Κούμερ, οι οποίοι επινοήθηκαν στο πλαίσιο της προσπάθειας του Κούμερ, το 1843, να αποδείξει το τελευταίο θεώρημα του Φερμά. (Σε μια εργασία του 1882, ο Ντέντεκιντ και ο Χάινριχ Μάρτιν Βέμπερ εφάρμοσαν τα ιδανικά σε επιφάνειες Ρίμαν, δίνοντας μια αλγεβρική απόδειξη του θεωρήματος Ρίμαν-Ροχ.

Το 1888 δημοσίευσε μια σύντομη μονογραφία με τίτλο Was sind und was sollen die Zahlen ("Τι είναι οι αριθμοί και για τι χρησιμεύουν;" Εβαλντ 1996: 790)^[18], η οποία περιελάμβανε τον ορισμό του για ένα άπειρο σύνολο. Πρότεινε επίσης μια αξιωματική θεμελίωση για τους φυσικούς αριθμούς, οι πρωταρχικές έννοιες της οποίας ήταν ο αριθμός ένα και η συνάρτηση διαδόχου. Τον επόμενο χρόνο, ο Τζιουζέππε Πεάνο, επικαλούμενος τον Ντέντεκιντ, διατύπωσε ένα σύνολο ισοδύναμων αλλά απλούστερων αξιωμάτων, τα οποία αποτελούν σήμερα τα καθιερωμένα αξιώματα.

Ο Ντέντεκιντ συνεισέφερε και σε άλλα πεδία της άλγεβρας. Για παράδειγμα, γύρω στο 1900 έγραψε τις πρώτες εργασίες για τα σπονδυλωτά πλέγματα. Το 1872, κατά τη διάρκεια των διακοπών του στο Ιντερλάκεν, ο Ντέντεκιντ συνάντησε τον Γκέοργκ Κάντορ. Ο Ντέντεκιντ έγινε ένας από τους πρώτους μαθηματικούς που θαύμασε το έργο του Κάντορ για τα άπειρα σύνολα και αποδείχθηκε πολύτιμος σύμμαχος στις διαμάχες του Κάντορ με τον Λέοπολντ Κρόνεκερ, ο οποίος ήταν φιλοσοφικά αντίθετος με τους διαπεραστικούς αριθμούς του Κάντορ^[19].

Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]

Bιβλιογραφία στην αγγλική γλώσσα:

• 1890. "Letter to Keferstein" in Jean van Heijenoort, 1967. A Source Book in Mathematical Logic, 1879–1931. Harvard Univ. Press: 98–103.
• 1963 (1901). Essays on the Theory of Numbers. Beman, W. W., ed. and trans. Dover. Contains English translations of Stetigkeit und irrationale Zahlen and Was sind und was sollen die Zahlen?
• 1996. Theory of Algebraic Integers. Stillwell, John, ed. and trans. Cambridge Uni. Press. A translation of Über die Theorie der ganzen algebraischen Zahlen.
• Ewald, William B., ed., 1996. From Kant to Hilbert: A Source Book in the Foundations of Mathematics, 2 vols. Oxford Uni. Press.
  • 1854. "On the introduction of new functions in mathematics," 754–61.
  • 1872. "Continuity and irrational numbers," 765–78. (translation of Stetigkeit...)
  • 1888. What are numbers and what should they be?, 787–832. (translation of Was sind und...)
  • 1872–82, 1899. Correspondence with Cantor, 843–77, 930–40.

Bιβλιογραφία στη γερμανική γλώσσα:

• Gesammelte mathematische Werke (Complete mathematical works, Vol. 1–3).^[20] Retrieved 5 August 2009.

Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]

1. ↑ ^{Άλμα πάνω, στο:1,0 1,1 1,2} Εθνική Βιβλιοθήκη της Γερμανίας: (Γερμανικά, Αγγλικά) Gemeinsame Normdatei. Ανακτήθηκε στις 9  Απριλίου 2014.
2. ↑ ^{Άλμα πάνω, στο:2,0 2,1 2,2} Εθνική Βιβλιοθήκη της Γαλλίας: (Γαλλικά) καθιερωμένοι όροι της Εθνικής Βιβλιοθήκης της Γαλλίας. 123734127. Ανακτήθηκε στις 26  Ιουνίου 2020.
3. ↑ ^{Άλμα πάνω, στο:3,0 3,1 3,2} MacTutor History of Mathematics archive. Ανακτήθηκε στις 22  Αυγούστου 2017.
4. ↑ Εθνική Βιβλιοθήκη της Γερμανίας: (Γερμανικά, Αγγλικά) Gemeinsame Normdatei. Ανακτήθηκε στις 10  Δεκεμβρίου 2014.
5. ↑ Εθνική Βιβλιοθήκη της Γερμανίας: (Γερμανικά, Αγγλικά) Gemeinsame Normdatei. Ανακτήθηκε στις 30  Δεκεμβρίου 2014.
6. ↑ ^{Άλμα πάνω, στο:6,0 6,1} www.w-volk.de/museum/grave58.htm.
7. ↑ Εθνική Βιβλιοθήκη της Γαλλίας: (Γαλλικά) καθιερωμένοι όροι της Εθνικής Βιβλιοθήκης της Γαλλίας. data.bnf.fr/ark:/12148/cb123734127. Ανακτήθηκε στις 10  Οκτωβρίου 2015.
8. ↑ (Αγγλικά) Mathematics Genealogy Project. 18233.
9. ↑ MacTutor History of Mathematics archive. www-history.mcs.st-andrews.ac.uk/Biographies/Dedekind.html. Ανακτήθηκε στις 6  Οκτωβρίου 2017.
10. ↑ Εθνική Βιβλιοθήκη της Γερμανίας: (Γερμανικά, Αγγλικά) Gemeinsame Normdatei. Ανακτήθηκε στις 25  Ιουνίου 2015.
11. ↑ Ανακτήθηκε στις 3  Ιουλίου 2019.
12. ↑ ^{Άλμα πάνω, στο:12,0 12,1} «Richard Dedekind - Biography». Maths History (στα Αγγλικά). Ανακτήθηκε στις 21 Ιουνίου 2023.
13. ↑ James, Ioan (2002). Remarkable Mathematicians. Cambridge University Press. σελ. 196. ISBN 978-0-521-52094-2.
14. ↑ Ewald, William B., ed. (1996) "Continuity and irrational numbers", p. 766 in From Kant to Hilbert: A Source Book in the Foundations of Mathematics, 2 vols. Oxford University Press. full text
15. ↑ «Richard Dedekind | German Mathematician & Number Theory Pioneer | Britannica». www.britannica.com (στα Αγγλικά). Ανακτήθηκε στις 21 Ιουνίου 2023.
16. ↑ The Nature and Meaning of Numbers. Essays on the Theory of Numbers. Dover (δημοσιεύτηκε 1963). 1901. Part III, Paragraph 32.
17. ↑ The Nature and Meaning of Numbers. Essays on the Theory of Numbers. Dover (δημοσιεύτηκε 1963). 1901. Part V, Paragraph 64.
18. ↑ Richard Dedekind (1888). Was sind und was sollen die Zahlen?. Braunschweig: Vieweg. Online available at: MPIWG GDZ UBS
19. ↑ Aczel, Amir D. (2001), The Mystery of the Aleph: Mathematics, the Kabbalah, and the Search for Infinity, Pocket Books nonfiction, Simon and Schuster, σελ. 102, ISBN 9780743422994.
20.  ↑ Bell, E. T. (1933). «Book Review: Richard Dedekind. Gesammelte mathematische Werke». Bulletin of the American Mathematical Society 39: 16–17. doi:10.1090/S0002-9904-1933-05535-0  

ΖΗΝΩΝ  ΠΑΠΑΖΑΧΟΣ